
There is one obvious reason Stephanie always loses and cheating is not one of those.
If you have taken microeconomics class in college, game theory is one of the important aspects of the course, which allows a person to strategically determine the choice with the best possible payoff given the possible risk/reward. In the game of rock, paper and scissors, Stephanie has to pick the best possible strategy (e.g. picking paper if Sora picks rock) to get the outcome she wants as picking the same or a move that will make her lose will give her the worst payoff. In game theory terms, the payoff matrix for this game is the following:
Note: I shared the correct explanation for what happened in Game Theory terms in the comments
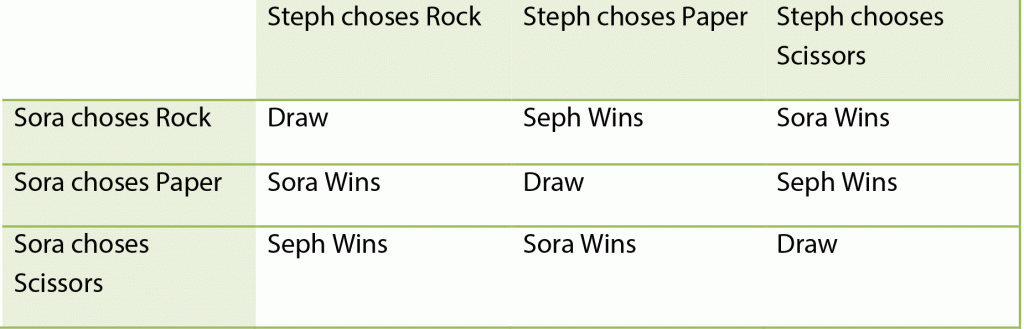
From this table, she should have taken the risk and predicted that Sora will play rock based on his prediction that his opponent will choose scissors from an assumption that he will always play paper. If she taken the risk and played paper, she would have a better payoff opposed to losing. The problem I see here is that she thinks that game theory is just about the outcomes and not coming up with the best strategy. Not only that, she is unwilling to take the risk even with the possibility that he won’t pick paper, which is the main reason she always loses. This is also apparent when she knew that her opponent, Kurami was cheating after he told her, but didn’t speak up. That, and her defeatist mentality due to humans having no magic is no wonder why Imanity is in such a dire situation.

Game theory aside, I still think this episode was very enjoyable. Besides the crude humor, which gave me some mixed feelings, I still like Shiro and Sora quite a lot even if his wish made his sister become a little jealous. Since the two knows everything about the kingdom, their main goal now is to now challenge Kurami for the position as king so that they can finally put Inamity back on the right track. From this, I hope that Sephanie will learn a thing from the two so that she won’t end up being a loser at games for the rest of her life.


But of course, Steph reading things one step further is moot if Sora reads her that she read that far and changes his own choice. The real issue is that Steph’s thought process is transparent to Sora (from her expression, etc.), rather than what that thought process actually is.
Aside from her making the decision based on Nash’s Equilibrium, which is the best possible outcome for her based on Sora’s decision, I agree that her emotions is what made it too obvious. She needs to learn to not make it too obvious (e.g. have a Poker face) so that Sora wouldn’t second guess her and ending up with a draw.
I think you misunderstand the rule of ROCk, PAPER, and SCISSORS in Sora’s game a bit. (Many people has this misunderstanding, don’t worry)
First of all, the game results was “Draw”. Sora didn’t win.
Remember that Sora said if he use anything beside Paper, he will lose. Sora always keep this rules, he didn’t say it to trick Stephanie that he’ll only use Paper.
He CAN used the ROCk and SCISSORS but he’ll automatically lost because he didn’t use PAPER – Stephanie knew and understood this – but since Stephanie will also lose if Sora win her with ROCK or SCISSORS in such case the game will be “draw” since both side lose. (This is one of the rules that Sora explained)
Now, Sora won Stephanie with Rock, therefore he “lost” but Stephanie also “lost” because she used SCISSORS againist ROCK. Thus, the game result became “draw” acccording to the Sora’s game rule.
(The win-lose table in your post is the table for “normal” ROCk, PAPER, and SCISSORS game not Sora’s game)
While the difference is relatively small, this is true. For example, the scissors-scissors scenario is a loss for Sora, rather than a draw.
While my analysis is flawed for the fact that you don’t normally see three choices in payoff matrixes, I realize that this game plays more like a game of chicken. To better explain this, let’s assume that this is a game of chicken where Sora and Stephanie has to choose to drive straight or swerve. If the two choses to drive straight, both players will crash and lose.
As in the Anime with Sora saying that he will always play paper, let’s assume that he chooses to go straight. For Stephanie, from his decision, she will choose to Swerve as it will be a better decision rather than to go straight and crash. This is considered Nash’s Equilibrium, which is the best possible outcome. The same would be true if Sora decides to go straight and Stephanie swerves. However, the only problem with Stephanie swerving is for the fact that players might have a different equilibrium.
Thus, the payoff table is this

Bold letters indicate Nash Equilibrium.
However, like in the Anime, Sora brinks and decides to swerve at the last second, thus resulting in a tie. Brinkmanship is typically used to prevent the other player from choosing the more aggressive behavior. As a result of changing his decision, it basically results in a tie where nobody crashes.
For Steph to win, she would have to realize that Sora will brink and decide to go straight instead. Of course, there is always a risk of him choosing to go straight as well. Better yet, she shouldn’t make it too obvious from her emotions.